Piero Della Francesca

13 février 2009

Piero della Francesca et son livre De prospectiva pingendi

Piero della Francesca (141?-1492) est un peintre et mathématicien italien. Son livre « De prospectiva pingendi » (tr. J.P. Le Goff, De la perspective en peinture. In Medias Res, 1998), rédigé vraisemblablement entre 1470 et 1485, est le premier traité consacré ouvertement à la perspective, et bien que seuls quelques exemplaires aient circulé, son retentissement a été considérable.
Il traite dans ce livre de la perspective des peintres, c’est-à-dire de la perspectiva artificialis. De même que le traité d’Alberti, son ouvrage est séparé en trois livres : le premier traite de la réduction des figures de la géométrie plane ; le second, de celle des volumes prismatiques ; dans le troisième enfin sont étudiés les volumes irréguliers tels que les chapiteaux, les coupoles et les têtes humaines. Bien que l’ouvrage s’adresse aux peintres, Francesca y utilise essentiellement un langage géométrique.

Dans une introduction au premier livre, l’auteur distingue trois parties dans la peinture : le dessin, la commensuration (la théorie des proportions), et la mise en couleurs. Le perspective est exactement la commensuration.
C’est ainsi qu’il écrit dans son premier livre que la projection - c’est-à-dire l’image que veut représenter le peintre, projetée sur sa toile - permet d’évaluer les grandeurs en considérant les triangles semblables. De plus, la « dégradation » d’une grandeur (la diminution relative de sa projection) est inversement proportionnelle à sa distance à l’œil. Cette théorie des proportions, qui règle les « dégradations » forme le véritable socle du traité.

Puis Francesca fait rapidement apparaître les premières mises en perspectives de figures planes. Tout d’abord le carré, puis le damier : il place le point de fuite « où il plaît », sans dépasser toutefois certaines limites évoquée au livre II. L’image du carré contenant le damier est tracée (il suffit pour cela de choisir une hauteur définissant la transversale la plus éloignée), ainsi que les lignes de fuite. La diagonale du carré image fournit alors l’image des transversales par ses intersections avec les lignes de fuites. Cette méthode simplifie considérablement celle d’Alberti, car elle ne nécessite aucune construction auxiliaire. De plus, si le tracé de la diagonale était une simple vérification chez Alberti, elle devient ici un principe de construction. Le point de distance n’est pas pour autant invoqué.

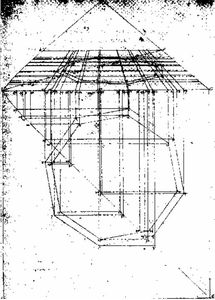
Voici quelques figures figurant dans son traité :