Albrecht Dürer

20 février 2009

Dürer et ses travaux sur la perspective

Albrecht Dürer (1471-1528) est un peintre, graveur et mathématicien allemand. Après un séjour en Italie, il se passionne pour les mathématiques. Il rédige l'ouvrage « Underweysung der Messung mit dem Zirkel und Richtscheit », imprimé en 1525 (Instruction sur la manière de mesurer à l'aide du compas et de l'équerre, tr. Peiffer J., Géométrie, Seuil, 1995) qui contient des gravures représentant des installations pour dessiner en perspective, comme le perspectographe dont il explique l'utilisation. Ce perspectographe est un outil qui permet de voir la scène à représenter au travers d'une vitre où les points importants sont reportés. Ainsi Dürer parle de « Durchsehung », c'est-à-dire « vue à travers ».

voir la page consacrée au perspectographe

voir la page consacrée à la mise en pratique de la fenêtre de Dürer

Les gravures ci-dessous illustrent dans son traité la façon de se servir de sa fameuse « fenêtre de Dürer » :

Cliquer sur les images pour les voir s'afficher en taille réelle.

Dans son traité, Dürer fait de la perspective centrale une science à part entière, impliquant recherches et démonstrations. Il y reprend la « construzione legittima » d'Alberti permettant de dessiner un carrelage en perspective puis dessine ensuite se qu'il appelle la « voie abrégée » qui reprend la technique d'Alberti tout en la simplifiant. Il décrit l'ombre portée en fonction de la direction de la source lumineuse. Les ombres portées prennent une place importante dans le traité de Dürer qu'il construit de la même manière que le carrelage d'Alberti. On peut noter qu'il associe ici lumière et perspective qui témoigne d'une volonté de ne pas séparer la représentation et la vue.

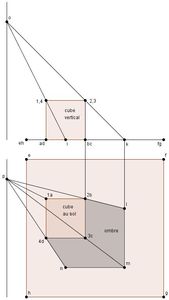
Dürer décrit dans son ouvrage la manière d'obtenir le tracé de l'ombre d'un cube. Il suffit de suivre les consignes énoncées :

« Construit donc un premier plan carré, efgh

« Construit donc un premier plan carré, efgh. Pose un cube sur le plan. Il y sera représenté par une surface carrée, car les quatre sommets supérieurs tombent sur les quatre inférieurs. C’est pourquoi chaque sommet aura une double désignation, les quatre sommets inférieurs seront appelés a, b, c, d et les quatre supérieurs 1, 2, 3, 4. C’est pourquoi ils se réunissent en a1, b2, c3, d4. Le plan inférieur est ainsi terminé.

Ce support carré avec le cube posé dessus, il convient maintenant de la faire monter comme un tailleur de pierre (architecte) fait monter dans le dessin, ses fondations à partir du plan.

Procède comme suit. Mène au-dessus du plan carré efgh un segment horizontal, parallèle au côté de ce plan, de même longueur et dont une extrémité est e, h et l’autre f, g. Ce segment signifie la même chose que le plan inférieur efgh et c’est pourquoi ses deux extrémités sont désignées par des lettres doubles.

Ensuite, élève des droites verticales issues des sommets a1, b2, c3, d4 du plan inférieur et prolonge-les d’une hauteur de cube au-delà de l’horizontale efgh. Tu détermineras ainsi la place qu’occupe le cube sur l’horizontale qu’on vient d’imaginer. L’arête inférieure du cube reposant sur le segment horizontal eh, fg, sera désignée par a, d à une extrémité et pas b, d de l’autre. L’arête supérieure sera 1, 4 et 2, 3. Ainsi les quatre sommets du cube dressés 1, 4 ; 2, 3 ; b, c ; a, d seront situés, ce qui est tout à fait compréhensible, au dessus de son plan inférieur.

Ensuite il convient de placer la source de lumière. Mais de même que j’ai construit deux plans, un plan abaissé et un plan dressé, je dois placer, dans chacun des plans, sa lumière particulière. Dans le plan dressé, je fixe la hauteur de la source lumineuse au-dessus ou au dessous du cube, et dans le plan abaissé je détermine sa distance latérale du cube ou je la place au milieu.

Ici cependant tu peux placer, dans le plan dressé, la lumière o à une distance et à une hauteur arbitraires.

Dans le plan abaissé, place la seconde lumière p de tel côté que tu voudras, mais fais en sorte que les deux lumières soient à la même distance latérale du cube abaissé et dressé. Ensuite mène deux rayons en ligne droite du point o de la lumière supérieure aux angles supérieurs du cube dressé 1, 4 et 2, 3. Marque les points où ces rayons tombent sur la droite e, f et g, h, par les lettres i et k. L’ombre portera jusque là. Ensuite, mène les rayons du point p de la lumière inférieure aux sommets du plan du cube, points désignés par b, 2 ; c, 3 ; d, 4. Laisse progresser les rayons. Les points d’intersections des lignes droites abaissées des points i et k avec les rayons de la lumière inférieurs qu’on vient de tracer dans le plan y indiqueront la longueur et la largeur de l’ombre. Désigne les extrémités de l’ombre par l, m, n. Relie ces points par des lignes droites. Relie de même b, 2 à l et d, 4 à n. Tu obtiendras ainsi le contour de l’ombre.

Remarque notamment que ces deux lumières ne font qu’une, comme la ligne d’extrémité e, f et f, g ne fait qu’un avec le plan efgh situé dessous, ainsi que je l’ai déjà dit plus haut. Les cubes abaissé et dressé ne forment de même qu’un seul objet. En somme, les deux plans et les deux lumières sont comme un objet mais scindé en deux pour faciliter l’usage. »